随机信号中标准差的3倍与5倍范围解析
在随机信号分析中,标准差(σ)是衡量信号波动程度的重要指标。以高斯白噪声为例,其概率密度函数呈正态分布,不同标准差倍数对应的覆盖范围和工程意义如下:
一、理论范围与覆盖概率
- ±3σ范围
覆盖约99.73%的数据,即信号值有99.73%的概率落在 μ-3σ 至 μ+3σ 之间(μ为均值)。超出此范围的概率仅为0.27%,通常视为小概率事件。 - ±5σ范围
覆盖约99.99994%的数据,信号值落在此范围的概率超过99.999%。超出5σ的极端情况概率仅为0.00006%,常用于极端异常检测。
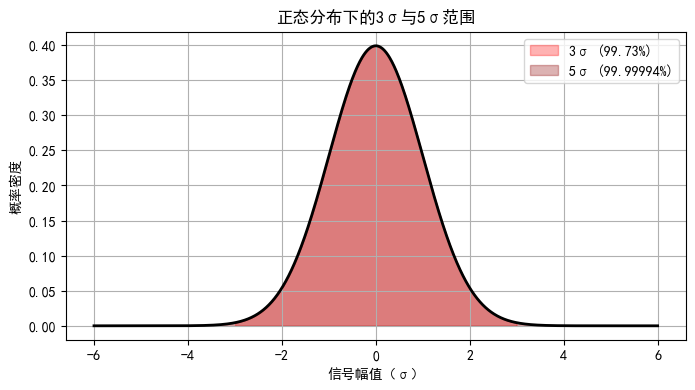
图1:正态分布曲线(阴影部分为±3σ和±5σ范围)
从时域信号的角度出发,对于高斯白噪声,由下图可见不同σ控制范围下,出现超出范围数据的概率情况:
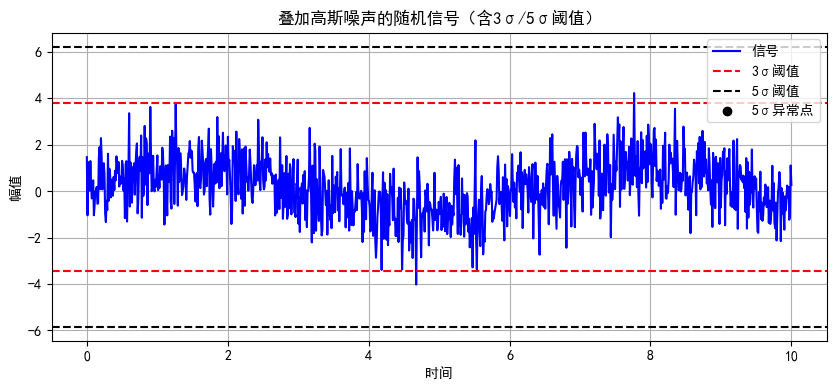
二、工程应用场景
- 质量控制
- 3σ原则:工业中常用于设定质量控制限,例如六西格玛管理中,3σ对应每百万次机会中出现2700次缺陷。
- 5σ原则:适用于高精度系统(如航天、医疗设备),确保极低故障率。
- 信号检测与滤波
- 在通信系统中,3σ可作为噪声门限,过滤大概率噪声;5σ则用于识别罕见事件(如突发干扰)。
- 金融风险管理
- 金融时间序列分析中,3σ和5σ分别对应市场极端波动的预警阈值。
三、总结
- 3σ范围:平衡误判率与漏检率,适用于常规监测。
- 5σ范围:追求极致可靠性,代价是更高的计算复杂度。
实际应用中需根据系统容错率与成本权衡选择阈值倍数。
通过上述分析可知,标准差倍数不仅是统计学概念,更是工程实践中控制风险、优化性能的核心工具。
