窗函数是减少泄露的有效手段之一,它通过对时域信号进行加权,将采集到的信号块由非周期信号转变为周期信号,使其满足傅里叶变换的周期性要求。
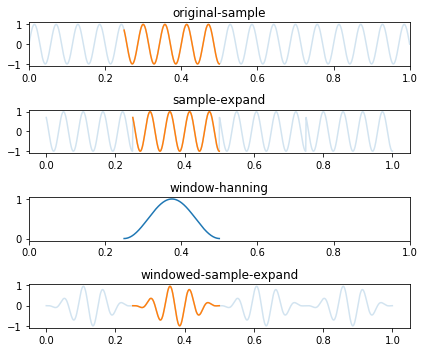
加窗的方法就是对采集到的信号进行时域加权:
x_{win}(n) = x(n) * win(n)根据傅里叶变换的性质可知,时域信号加窗,相当于信号频谱与窗函数频谱的卷积。
常用的窗函数主要有:
– 矩形窗
– 汉宁窗
– 平顶窗
– Blackman-Harris
– Kaiser-Bessel
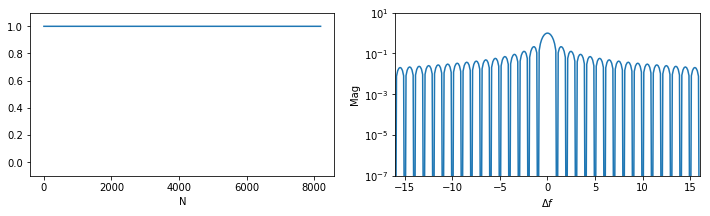
矩形窗
矩形窗上各点均是1,也就是不加窗。
w(n) = 1, n\in[0, N-1]其中n为索引,N为采样点数,其时域和频域如下图所示:
汉宁窗
w(n) = 0.5(1-cos(\frac{2{\pi}n}{N-1})), n\in[0, N-1]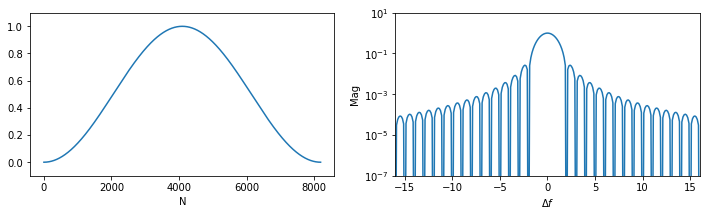
平顶窗
w(n) = (1-1.93cos(\frac{2{\pi}n}{N-1})+1.29cos(\frac{4{\pi}n}{N-1})-0.388cos(\frac{6{\pi}n}{N-1})+0.0322cos(\frac{8{\pi}n}{N-1}))/4.634, n\in[0, N-1]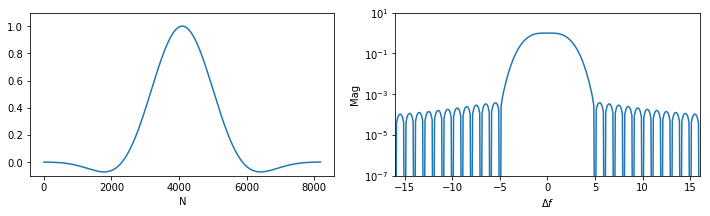
Blackman-Harris
w(n) = 0.35875 - 0.48829cos(\frac{2{\pi}n}{N-1})+0.14128cos(\frac{4{\pi}n}{N-1})-0.01168cos(\frac{6{\pi}n}{N-1})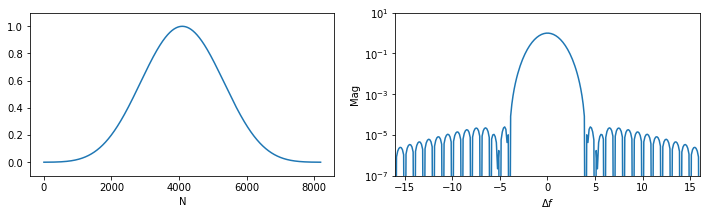
Kaiser-Bessel
w(n) = 0.40243 - 0.49804cos(\frac{2{\pi}n}{N-1})+0.09831cos(\frac{4{\pi}n}{N-1})-0.00122cos(\frac{6{\pi}n}{N-1})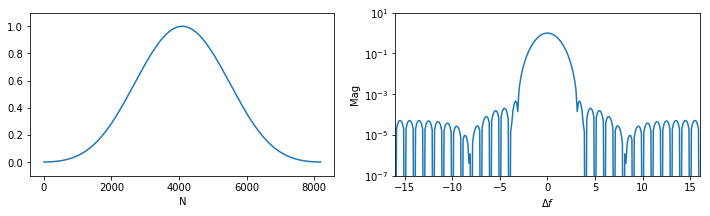
窗函数的影响
因为加窗相当于对被测信号频域上的卷积,结果相当于将窗函数频谱平移到原信号频谱后的加权叠加,也就是将原频域信号沿着窗函数频域曲线泄露了出去,窗函数的主瓣宽度和旁瓣衰减直接影响了窗函数的性能。
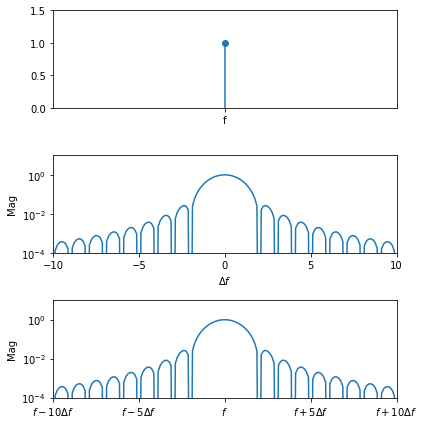
考虑到数字信号处理仅计算n{\Delta}f各点的值,因此当被测信号频率靠近n{\Delta}f时泄露较小,而靠近(n + 1/2){\Delta}f时泄露较大。
窗函数的主瓣宽度越大,频谱的幅值就越接近被测信号,但是同时距离较近的频率就越难被分辨出来。旁瓣衰减的越快则由旁瓣带来的泄露也越小。
总结
窗函数的区别主要考虑其主瓣宽度和旁瓣衰减。主瓣的顶部宽度越宽,对幅值测量的精度越高。主瓣宽度和旁瓣的衰减同时影响频率的分辨能力,主瓣宽度越小、旁瓣衰减越快,对频率的分辨能力越强,泄露的程度就越小。在使用过程中应该根据测试的实际情况选择合适窗函数。通常情况下矩形窗适合被测信号自身可以保证整周期采样的情况,如力锤敲击等;随机信号可选用汉宁窗,可以同时兼顾幅值精度和分辨能力;平顶窗适合校准等幅值需要精确测量的情况。
